Table of Contents
Numerical Optimization Techniques and Dynamic Programming Lagrange Multipliers Knapsack
Dynamic programming
Dynamic programming is an optimization approach that converts a complex problem into a sequence of simpler problems; its crucial feature is the multistage nature of the optimization method
Dynamic Programming solves every sub-problem just once and stores the result into a table so that it can be easily recovered if we need it again. Dynamic Programming is a Bottom-up approach by which we can solve every possible small problem and then merge to obtain solutions for larger problems.
EXAMPLE
SOLVE THE FOLLOWING LPP USING DPP:
Maximize z = 5x1 + 9x2
subject to
−x1 + 5x2 ≤ 3
5x1 + 3x2 ≤ 27
x1, x2 ≥0
Solution:
A/Q
−x1 + 5x2 ≤ 3 ………..eq(i)
5x1 + 3x2 ≤ 27 ………..eq(ii)
Let B1 & B2 be the resources associated with the 1st and 2nd constraints respectively.
B1= 3 & B2 = 27.
From eq (i), 5x2 has to be ≤ to R1, i.e., x2 ≤R1/5.
Similarly, from eq (ii), we have
X2 ≤R2/3.
Now, we are maximizing, the maximum value of x2 has to be = minimum of R1/5 and R2/3.
ƒ2(R1, R2)= Max (9x2)
= 9 Max (x2)
= 9 Min (R1/5,R2/3)−−−−−−−eq(iii)
ƒ1(3, 27)= Max [5x1 + ƒ2(3 + x1, 27 – 5x1)]−−−−−−eq(iv)
0 ≤ x1 ≤27/5
From equation (iii),
ƒ2(R1,R2)= 9 Min (R1/5,R2/3)−−−−(iv)
Now, ƒ2(3 + x1, 27 – 5x1)= 9 Min [(3 + x1)/5 ; (27 – 5x1)/3]
From eqn (iv)
ƒ1(3, 27)= Max {5x1 + 9 Min[(3 + x1)/5,(27 − 5x1)/3]}−−−−−eq(v)
We now find the range of x1 for which (3 + x1)/5<(27 – 5x1)/3.
NOW, Comparing (3 + x1)/5 & (27 – 5x1)/3, we get
(3 + x1)/5 = (27 – 5x1)/3
3(3 + x1)= 5(27 – 5x1)
9 + 3x1 = 135 – 25x1
∴ x1 =9/2
From eqn (v), we have
ƒ1(3,27)= Max [5x1 +9(3 + x1)/5]
if x1 ≤9/2
=> Max [5x1 +9(27 − 5x1)/3]
if x1 >9/2
From the above, the maximum occurs at x1 =9/2
x2 = Min [3 + 9/2)/5 ,(27 – 5 X 9/2)/3]
=> Min (15/10,9/6)= Min (1.5,1.5)=1.5
Hence, the optimal solution is
x1 = 4.5 , x2 = 1.5
z = 5 X 4.5 + 9 X 1.5 = 22.5 + 13.5 = 36
SOLVE THE SAME QUESTION USING CALCULATOR
STEPS OF DYNAMIC PROGRAMMING PROBLEMS
- Stages: The problem can be divided into a number of different sub-problems which are called stages. A stage is a small part of given problem.
- States: These are variables which are used for taking a decision at every stage which is called state variable.
- Decision: The decision which taken at each n every stage should be optimal this is known as a stage decision.
- Optimical Policy: It is a policy which decides the decision at each n every stage called an optimal policy and known as Bellman principle of optimality.
Applications of dynamic programming to solve the following problem:
- 0/1 knapsack problem
- Mathematical optimization problem
- All pair Shortest path problem
- Reliability design problem
- Longest common subsequence
- Flight control and robotics control
- Time sharing: the job to maximize CPU usage
Lagrange Multipliers
Lagrange multipliers can be used for optimizing issues and open equity issues such as:
Maximize f(x,y)
Subject to constraint
g(x,y)=0
To solve these problems clearly, we need both f and g to have a continuous first phase. A new variant (λ) called the Lagrange multiplier is introduced and solves the Lagrange function defined as:
L(x,y, λ) = f(x,y) – λ g(x,y)
Q.Find the maximum and minimum values of f(x,y)=81x2+y2 subject to the constraint 4x2+y2=9
sol:
Form the Lagrangian: L(x,y,λ)=(81×2+y2)+λ(4×2+y2−9)
first−order partial derivatives:
∂L((81x2+y2)+λ(4x2+y2−9))/∂x= 2x(4λ+81)…….eq(1)
∂L((81x2+y2)+λ(4x2+y2−9))/∂y= 2y(λ+1)……eq(2)
∂L((81x2+y2)+λ(4x2+y2−9))/∂λ= 4x2+y2−9…….eq(3)
From eq(1), eq(2)and eq(3)we get,
(x,y)=(−3/2,0), (x,y)=(0,−3)
(x,y)=(0,3), (x,y)=(3/2,0)
Putting value of x and y in fn f(x) ;
f(−3/2,0)=729/4
f(0,−3)=9
f(0,3)=9
f(3/2,0)=729/4
The absolute maximum is then 729/4=182.25
which occurs at (−3/2,0) and(3/2,0).
The absolute minimum is 9 which occurs at (0,−3) and (0,3)
CHECK THIS SAME PROBLEM USING A CALCULATOR:
Gomory Cutting Plane Method
• Consider standard Linear Programming problem with all variables restricted to integers
• Basic strategy:
a) use a simplex algorithm to solve LP
Consider the linear program
b) iteratively add constraints to find optimal integer soln.
EXAMPLE OF CUTTING PLANE METHOD:
min z = 2x1 +15x2 +18x3
Subject to:
-x1+2x2-6x3<= -10
x2+2x3<=6
2x1+10x3<=19
-x1+x2<=-2
x1, x2, x3>=0
We can solve this problem with the dual simplex method algorithm. The final tableau is as follows:

If all the variables are integers, we also have that
-2x2+x3,-z1-z3<=[1/2]
-2x2+x3 – z1-z3<=0
We can add this new inequality to our tableau in the form
-2x2+x3– z1-z3+z5=0
Inserting this inequality into our tableau, we obtain
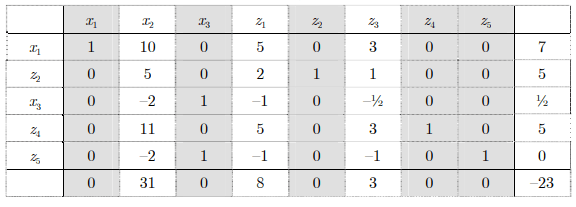
The matrix in the body of the tableau is A
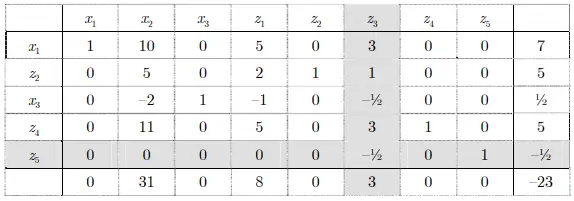
z5 is negative, and we, therefore, pivot on that row. The only column with a negative entry in that row is z3, so we pivot there.
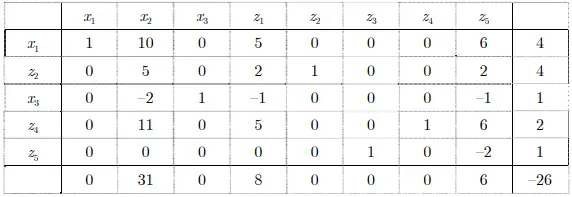
This solution is both primal and dual optimal, with only an integer solution.
x1=4
x2=0 Objective function = 26
x3=1
CHECK THE SAME PROBLEM USING A CALCULATOR:
Branch and Bound method
The Branch and Bound method is not a limited solution to system problems that are part of the whole. It is a solution that can be applied to different kinds of problems. The branch and bound approach and responsibility are based on the principle that the sum of possible solutions can be sub-divided into smaller parts of solutions. These smaller sets can be re-evaluated systematically until a better solution is found. If the branch and bound method is used in a complete planning problem, it is used in conjunction with the standard non-integer solution.
Find solution using Branch and Bound method
MAX z = 5x1+6x2
subject to
x1+x2 <= 5
4x1+7x2 <= 28
and x1, x2 >= 0
x1 and x2 are integer
ANSWER:
Z=27 and x1=3, x2=2
CHECK THE SAME PROBLEM USING A Branch and Bound Method CALCULATOR:
Knapsack
The Knapsack algorithm determines the number of each item be included in the collection so that the total weight is less or equal to a certain limit and the total value is as large as possible.
Although in Knapsack 0-1 the elements of the algorithm cannot be separated which means that the whole thing has to be taken away or abandoned.
Example Question
Profit = [ 20, 5, 10, 40, 15, 25 ]
weight = [ 1, 2, 3, 8, 7, 4 ]
Max W = 10
IF WE WILL SOLVE THE SAME PROBLEM USING KNAPSACK AND KNAPSACK 0-1 WE GET PROFITS OF 70 AND 60 RESPECTIVELY.
MAX PROFIT IS 70.
YOU CAN CHECK THIS PROBLEM USING CALCULATOR(Link Given Below)
https://augustineaykara.github.io/Knapsack-Calculator/
Wolfe’s Method
Quadratic programming is a special type of indirect programming with special features; that is, objective work is quadratic forms and barrier functions are linear functions.
This method converts the quadratic problem into the linear problem. Wolfe fixed an easy way to solve the quadratic system problem by adding Karush-Kuhn-Tucker (KKT) scenarios and transforming the purpose function of quadratic forms into line form.
Example Question of Wolfe’s Method
Max Z=8x1+10x2–2x12-x22 subject to 3x1+2x2<=6 and x1, x2 >=0
ANSWER
The optimum solution is x1=4/17, x2=45/17, z is max(z) = 6137/289.
YOU CAN CHECK THIS PROBLEM USING THIS CALCULATOR:
https://www.wolframalpha.com/widgets/gallery/view.jsp?id=311514b82e2e45f6fcbf6b09217dcf8d
0-1 IMPLICIT ENUMERATION TECHNIQUE / ADDITIVE ALOGRITHM
Example Question of 0-1 IMPLICIT ENUMERATION TECHNIQUE
Minimization: Z = 5X₁ + 6X₂ + 10X3 + 7X4 + 19X5
Subject to:
5X₁ + X₂ + 3X₂ – 4X4 + 3X5 ≥ 2
-2X₁ + 5X₂ – 2X3 – 3X4 + 4X5 >=0
X₁ – 2X₂ – 5X3 + 3X4 + 4X5 ≥ 2
X₁ = 0 or 1 for all j = 1,2,3,4,5
ANSWER
FEASIBLE SOLUTION Z=18 AT X₁=X₂=X4=1
YOU CAN CHECK THIS PROBLEM USING THE CALCULATOR
Stochastic Linear Programming Model
Question
MAX Z= 5x1 +10x2 -4x3 -6x4
subject to x3 + x4 = 10
x1 + 3x2 <= 14
and x1,x2,x3, x4 >= 0
YOU CAN CHECK THIS PROBLEM USING THE CALCULATOR
Also Read


THANKS FOR THIS